En matemáticas, los números reales incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a los números irracionales aquellos que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periodicas, tales como: 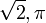. Números reales son aquellos que poseen una expresión decimal.

Pueden ser descritos de varias formas, aparentemente simples, pero estas carecen del rigor necesario para los propósitos formales de matemáticas.

Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, usando expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó finalmente a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa a la nueva matemática, la cual incluyó definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.^[1] Más adelante se describirán algunas de las definiciones más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales, Cortaduras de Dedekind




 

Si es un número racional donde p/q está reducido a sus términos mínimos (sin factor común) entonces 2q²=p².

La expresión anterior indica que p² es un número par y por tanto p también, es decir, p=2m. Sustituyendo obtenemos 2q²=(2m)²=4m², y por tanto q²=2p².

Pero el mismo argumento usado nos dice ahora que q debe ser un número par, esto es, q=2n. Mas esto es imposible, puesto que p y q no tienen factores comunes (y hemos encontrado que 2 es un factor de ambos).

Por tanto, la suposición misma de que es un número racional debe ser falsa.